CC-SubD — Catmull‑Clark細分曲面の精密評価（MATLAB実装）

Library
CC-SubD — Catmull‑Clark細分曲面の精密評価（MATLAB実装）

CC-SubD — Catmull‑Clark細分曲面の精密評価（MATLAB実装）

本リポジトリは、Catmull‑Clark細分曲面の「精確評価（exact evaluation）」を実装したMATLABツールキットです。基底関数（basis function）とその微分を高精度に求められることを目的とし、細分面を用いた等幾何解析（isogeometric analysis）や解析前処理での基礎ライブラリとして利用できます。サブディレクトリに評価・基底解法・要素探索の機能が整理されています（約300字）。

https://github.com/Jinlz0428/CC-SubD

概要

CC-SubDはCatmull‑Clark細分曲面の「精確評価」を行うためのMATLAB実装です。目標は基底関数（basis functions）とその偏導関数を安定かつ正確に算出し、細分ベースの等幾何解析（subdivision‑based isogeometric analysis）研究や応用実装を支援することにあります。リポジトリには基底計算、点と偏導の評価、要素検索に関する関数群が整理されており、研究用途のプロトタイプとして手早く活用できます（約300字）。

GitHub

リポジトリの統計情報

  • スター数: 1
  • フォーク数: 0
  • ウォッチャー数: 1
  • コミット数: 4
  • ファイル数: 4
  • メインの言語: MATLAB

主な特徴

  • Catmull‑Clark細分曲面の基底関数とその偏導関数を精確に評価する機能。
  • 基底関数計算（subd_basis）、点と微分の評価（subd_eval）、要素探索（subd_find）など機能ごとに整理されたモジュール構成。
  • 等幾何解析など、細分曲面を解析空間として使う研究に適したツールセット。
  • MATLABで実装されており、研究者や教育用途で扱いやすいプロトタイプ。

技術的なポイント

本プロジェクトは「精確評価（exact evaluation）」という用語が示す通り、有限回の繰り返しによる近似的評価ではなく、特に特異点（extraordinary vertex）周りの極限形状やその微分を理論的に正確に求める手法群を実装することを目指しています。一般にCatmull‑Clark細分の精確評価では、局所的な細分作用素の固有値・固有ベクトル解析（固有分解）を用い、主軸方向（characteristic map）や制御点からの寄与（stencils）を明示的に計算する必要があります。本リポジトリではこれらをMATLABで扱いやすい形にまとめ、基底関数の値と一階・二階の偏導を安定して算出できるようにしている点が注目されます。 また、要素検索（element search）機能を備えており、パラメトリック座標系やメッシュ要素に対する点の所属判定を行えるため、解析メッシュとの連携や積分点の配置に利用できます。等幾何解析との親和性を考慮すると、基底の局所サポートや滑らかさ（C1連続性の扱い）・特異点処理が重要で、本実装はこれらの基礎計算を提供することで、既存の解析コードに組み込みやすい基盤となります。加えて、MATLAB実装によりデバッグや可視化が容易で、教育的なデモやプロトタイピングに向いています。

プロジェクトの構成

主要なファイルとディレクトリ：

  • LICENSE: file
  • README.md: file
  • pictures: dir
  • src: dir

（README抜粋より）主なサブディレクトリ構造の例：

  • subd_basis \ 計算細分曲面基関数
  • subd_eval \ 計算細分曲面点と偏導ベクトル
  • subd_find \ 要素検索に関する関数群
  • subd_ini… \ 初期化やユーティリティ（想定）

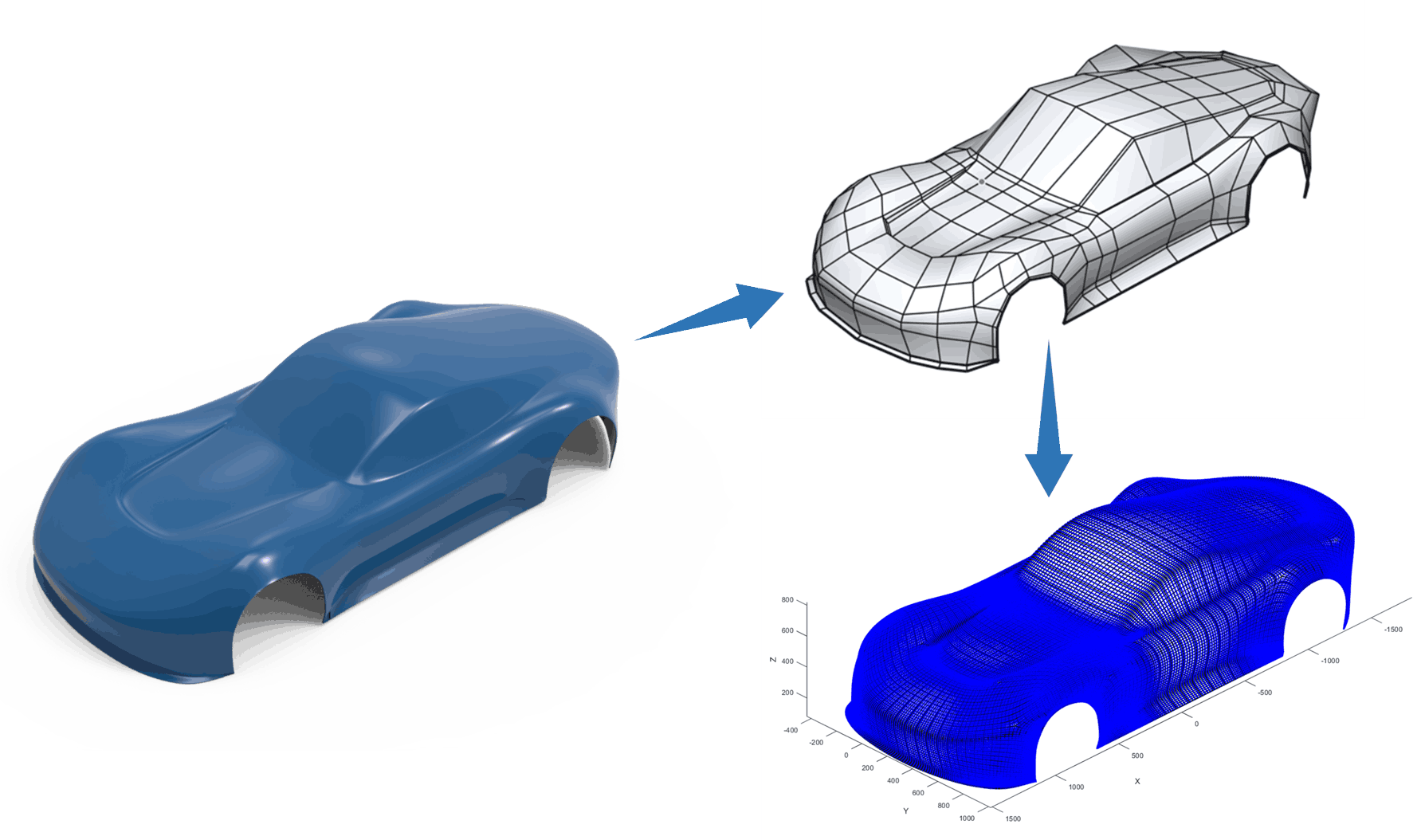
READMEにはプロジェクトの目的（基底関数の解法ツール、等幾何解析支援）とサンプル画像が含まれており、コードの使い方・例のスクリプトを整備すると実用性が高まります。

利用シーンと拡張提案

  • 利用シーン:
    • 細分曲面を解析空間として用いる等幾何解析（IGA）の前処理。
    • 学術研究における基底関数の検証や比較研究。
    • 教育用途での細分理論の可視化と実験。
  • 拡張提案:
    • サンプルワークフロー（メッシュ入力→基底評価→数値積分）を含むデモスクリプト追加。
    • パフォーマンス向上のためにホットスポットをC/MEX化、あるいは並列化の検討。
    • 境界条件処理や特殊ケース（開いた境界、非四面体混合など）への対応拡張。
    • Python/C++バインディングの提供で他言語エコシステムとの連携強化。

まとめ

Catmull‑Clark細分の精確評価に特化した研究用MATLABツールで、等幾何解析の基盤として有用。拡張で実用性がさらに向上する。

リポジトリ情報：

READMEの抜粋：

CC-SubD

该程序实现了Catmull-Clark细分曲面的精确评估，旨在为求解基函数提供一个稳健的工具，以支持基于细分的等几何分析的相关工作。

This program implements the exact evaluation of Catmull-Clark subdivision surfaces, aiming to provide a robust tool for solving basis function to support related work of subdivision-based isogeometric analysis.

这是图片